记录时间：2022-08-08 17:37
每日学习笔记
数学
分部积分法的推广公式（连续多次套娃）：
一般使用画表格的方式来解决问题
需要多写几次以记住的部分。
- 为什么三和指可以互换？（反对幂三指）
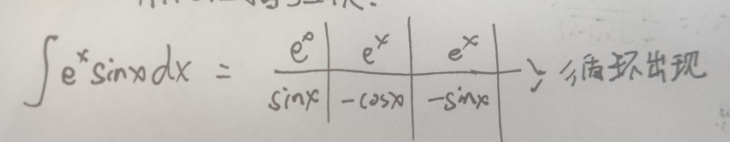在进行多次公式使用时，这两个函数都会呈现循环出现的情况。
当然了据此可以推出：
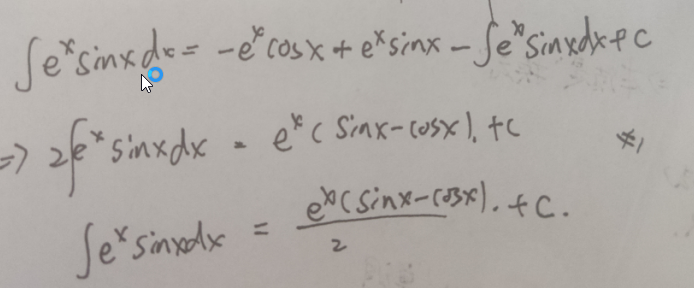
化简得：
\[\int{e^{x}sinxdx}= \frac{e^x(sinx-cosx)}{2}\](并未提及是什么重要结论)
有理函数积分
对于$\int{\frac{P_{n}(x)}{Q_{m}(x)}}dx$的情况，若$n<m$ 则对$Q_{m}(x)$进行因式分解（注意分解出来的要是实数域，如果分不出来，可以换 每日学习笔记-2022-08-06 的凑微分法。
考研不会极难，如果分解不出来，更大的可能是方法有问题。
要求：
总结：一和二次因式，按整体看，一次就产生一次，若多次，一路展过去$x,x^2,x^3…$
例题：
\(\int{\frac{4x^2-6x-1}{(x+1)(2x-1)^2}}\)
这种就是类似分解好的情况，可以直接分成：
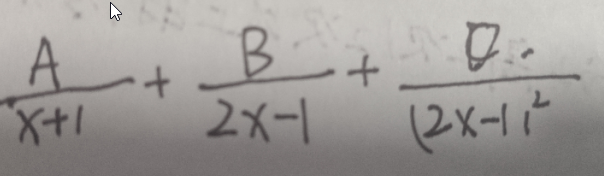之后“代入一些特殊值，去解ABD出来，解出来之后就好处理了。
例题8.21 为 需要练习的题目。